
The standard error of the mean is the expected value of the standard deviation of means of several samples, this is estimated from a single sample as:Ĭopyright © 2000-2021 StatsDirect Limited, all rights reserved. If a variable y is a linear (y = a + bx) transformation of x then the variance of y is b² times the variance of x and the standard deviation of y is b times the variance of x. The standard error is equal to the square root of the sampling variance, i.e.: This means that the sampling distribution on the HISEI mean for Germany has a. When distributions are approximately normal, SD is a better measure of spread because it is less susceptible to sampling fluctuation than (semi-)interquartile range. For any symmetrical (not skewed) distribution, half of its values will lie one semi-interquartile range either side of the median, i.e. Semi-interquartile range is half of the difference between the 25th and 75th centiles. Interquartile range is the difference between the 25th and 75th centiles. When we were discussing the sampling distribution of sample proportions, we said that this distribution is approximately normal if np 10 and n(1 p) 10. Now we will investigate the shape of the sampling distribution of sample means. It is a measure of the extent to which data varies from the mean. Let’s compare and contrast what we now know about the sampling distributions for sample means and sample proportions. (a) Construct and interpret a 99 confidence interval for the difference in the true proportions of men and women aged 19. (Ref: ) The survey found that 986 of the men and 923 of the women lived in their parents’ home. Standard Deviation is square root of variance. A random sample by the National Institutes of Health included 2253 men and 2629 women who were between the age of 19 and 25. Where is Mean, N is the total number of elements or frequency of distribution. This is not the case when there are extreme values in a distribution or when the distribution is skewed, in these situations interquartile range or semi-interquartile are preferred measures of spread. First, calculate the deviations of each data point from the mean, and square the result of each: variance 4. SD is the best measure of spread of an approximately normal distribution. All three terms mean the extent to which values in a distribution differ from one another. The spread of a distribution is also referred to as dispersion and variability. The unbiased estimate of population variance calculated from a sample is: Variance is usually estimated from a sample drawn from a population. SD is calculated as the square root of the variance (the average squared deviation from the mean). Standard error decreases when sample size increases – as the sample size gets closer to the true size of the population, the sample means cluster more and more around the true population mean.The standard deviation of the mean (SD) is the most commonly used measure of the spread of values in a distribution. Indeed, Se will usually be smaller than SY because the. the variance of the population, increases. The first formula shows how Se is computed by reducing SY according to the correlation and sample size. Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services. Standard error increases when standard deviation, i.e. Discover How We Assist to Edit Your Dissertation Chapters. Standard error can be calculated using the formula below, where σ represents standard deviation and n represents sample size.
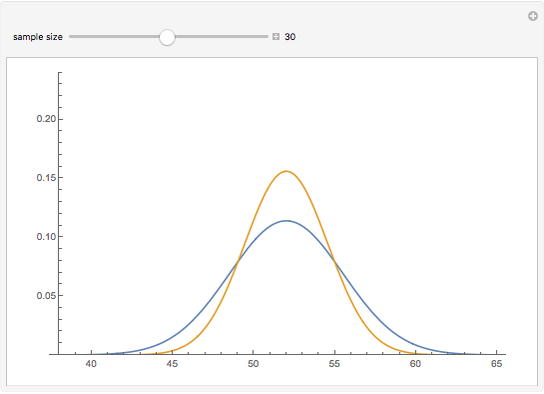
the means are more spread out, it becomes more likely that any given mean is an inaccurate representation of the true population mean.

The standard error tells you how accurate the mean of any given sample from that population is likely to be compared to the true population mean. the standard deviation of sample means, is called the standard error. The standard deviation of this distribution, i.e. If you take enough samples from a population, the means will be arranged into a distribution around the true population mean. Because of this, you are likely to end up with slightly different sets of values with slightly different means each time. When you are conducting research, you often only collect data of a small sample of the whole population. Divide the sum by the number of values in the data set.For each value, find the square of this distance.For each value, find its distance to the mean.The steps in calculating the standard deviation are as follows: It can, however, be done using the formula below, where x represents a value in a data set, μ represents the mean of the data set and N represents the number of values in the data set. Standard deviation is rarely calculated by hand. In any distribution, about 95% of values will be within 2 standard deviations of the mean.
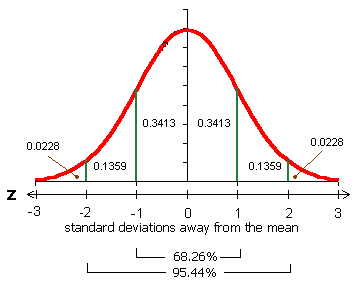
It is a measure of how far each observed value is from the mean. Standard deviation tells you how spread out the data is.


 0 kommentar(er)
0 kommentar(er)
